쾨니히스베르크 다리 문제와 그래프 이론의 시작

수리: (노트북을 열며) 오늘은 쾨니히스베르크 다리 문제와 그래프 이론의 시작에 대해 이야기해볼까 해. 이 문제는 수학의 새로운 분야를 열었고, 현대 컴퓨터 과학과 네트워크 이론의 기초가 됐어.

인문: 쾨니히스베르크 다리 문제? 그게 뭔데?

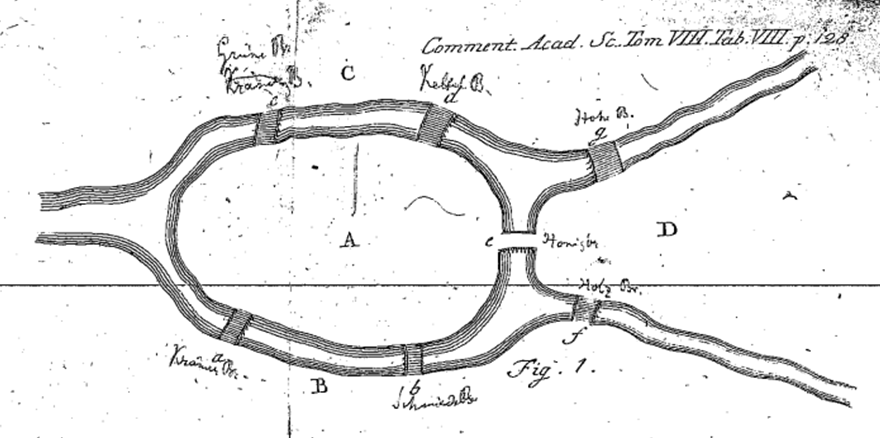
수리: 18세기 프로이센의 쾨니히스베르크라는 도시에는 강이 흐르고 있었어. 이 강에는 두 개의 섬이 있었고, 섬과 육지를 연결하는 총 7개의 다리가 있었지. 사람들은 이 다리들을 한 번씩만 건너면서 모든 다리를 지나갈 수 있는지 궁금해했어.

통섭: 그런데 그게 왜 수학적 문제가 되는 거야?

수리: 이 문제는 단순한 퍼즐처럼 보이지만, 수학적으로 접근하면 아주 중요한 개념을 배울 수 있어. 바로 그래프 이론의 시작이야. 오일러는 이 문제를 해결하기 위해 도시의 지도를 수학적 모델로 변환했어.

뮤지: 그래프 이론이 뭔데?

수리: 그래프 이론은 점(vertex)과 선(edge)으로 이루어진 구조를 연구하는 수학 분야야. 쾨니히스베르크 다리 문제에서는 섬과 육지를 점으로, 다리를 선으로 표현할 수 있어. 이렇게 하면 문제를 추상적으로 분석할 수 있지.

인문: 그럼 오일러는 어떻게 이 문제를 해결했는데?

수리: 오일러는 각 점에 연결된 선의 개수를 세어서 해결했어. 만약 어떤 점에 연결된 선의 개수가 홀수라면, 그 점은 출발점이나 도착점이 돼야 해. 쾨니히스베르크 다리 문제에서는 홀수 개의 선이 연결된 점이 4개나 있었어. 그래서 모든 다리를 한 번씩만 건너는 경로는 불가능하다는 결론을 내렸지.

통섭: 와, 그런데 이게 왜 그래프 이론의 시작이 됐다고?

수리: 오일러의 해결법은 단순한 퍼즐을 넘어, 수학적 구조를 분석하는 새로운 방법을 제시했어. 이건 네트워크, 지도, 심지어 소셜 미디어 연결까지 분석하는 데 쓰이는 그래프 이론의 기초가 됐지.

뮤지: 그럼 음악에서도 그래프 이론이 쓰이나?

수리: 그렇지! 음악에서 화음의 진행이나 멜로디의 구조를 그래프로 표현할 수 있어. 예를 들어, 각 음을 점으로, 음과 음 사이의 관계를 선으로 표현하면 음악의 구조를 수학적으로 분석할 수 있지.

인문: 그럼 이 문제는 단순한 퍼즐을 넘어, 인간의 사고를 확장시킨 거네.

수리: 맞아! 오일러의 해결법은 수학적 사고의 힘을 보여줬어. 그리고 이건 현대 컴퓨터 과학, 물류, 심지어 생물학에서도 중요한 도구로 쓰이고 있어.

통섭: 그래프 이론이 없었다면 현대 기술도 없었을 거야. 정말 혁명적인 발견이네.

뮤지: 그럼 쾨니히스베르크 다리 문제는 단순한 퍼즐이 아니라, 수학의 새로운 장을 연 출발점인 거네.

수리: 그렇지! 이 문제는 수학이 현실의 문제를 어떻게 해결할 수 있는지 보여주는 훌륭한 예야. 그리고 이걸 통해 우리도 복잡한 문제를 단순하게 바라보는 법을 배울 수 있지.

인문: 쾨니히스베르크 다리 문제는 단순한 수학적 문제를 넘어, 인간의 창의력과 논리적 사고를 보여주는 상징이야. 이걸 통해 우리도 문제를 새로운 시각으로 바라보는 법을 배울 수 있겠네.